The dynamic sun
published: KFKI-1996-02/CContent
1.0 Questions
A number after a question shows the page(s) of the book The Electric Universe on which the answer is to be found.
A fat number shows a picture. Fat letters show an important question. The questions below will reveal that this thick book is the sum of many short papers. All of them became explicable through the recognizing of the role of the electric force in the Universe. Therefore these models complete and prove each other. The specialists know that the present, non-electric astronomy cannot answer many questions - e.g. "What is the cause of the jets of the T-Tauri stars ? " S&T 1999 Jan.p.40. Mostly, an answer was missing in the past in the case of antigravitational motions due to electric repulsion (e.g. wind, corona, flare, CME, jets). Questions have now an answer also in the cases of the electric attraction (e.g. slow solar wind, helmet streamers, cosmic rays, flux tubes, solar loops in almost horizontal layers). Let us start with the most important investigation of our future:
1.1 Earth
1.1.1 Climate catastrophe
Why does the Sun heat stronger during the years of the cold sunspots ? 50, 48-51, 109-111
Why does our biosphere get warmer since the year 1715 ? 634, 634-636
Why does our biosphere get warmer monotonously since 1840 ? 634, 637, 630-639
How could the temperature jump upwards by 10 K within ten years ? 352, 353, 628, 631-633
Why is a culmination of the temperature in about 2040 predictable ? 355, 356-358, 627-640
How can we avoid the climate catastrophe ? 638-639
How does the tectonics sustain the biosphere ? 416
top of page
1.1.2 Tectonics
What is the common factor of the lava-whirls in the Earth and of the solar whirls ? 400
Why are the terrestrial and solar magnetic fields nearly parallel to the rotational axes ? 400
Why are the ridges mostly in the depth of the oceans ? 401-404, 402, 403, 404
Which theory of tectonics did the rotation of the Earth take into account ? 72-76
Why does the Earth not have bigger volcanoes than Mars ? 407
Why is Eurasia the biggest continent ? 414
Why are all oceans deeper southwards ? 410
Why are the south of the continents narrow ? 410
Why are more oceans on the southern hemisphere ? 410
Why do the ridges cross the equator mainly perpendicularly ? 402, 403, 406
Why was the global magnetic field almost parallel or antiparallel to the ridges ? 407
Why does a ridge exist around Antarctica , but none around the northern Pole ? 402, 408
Why do the plates move ? 404, 405, 409
Why are ridges fortunately not in the vicinity of the subduction ? 402, 403, 413
Why is the young Pacific-plate smooth but the old one wavy ? 403, 415, 413
Why do the plates not sink continuously, but suddenly ? 404, 415, 412
Why do the plates sink below the continents ? 402, 412
Why do most of the subduction-zones lie in a north-south direction ? 412, 404, 405, 415
Why does the Atlantic ridge consist of about 140 north-south elements ? 402, 403, 412
Why does the Atlantic ocean not have subduction-zones ? 412, 402, 415
Why is the Pacific ocean larger than the Atlantic ocean ? 414, 415
Was the cavity of the Pacific ocean originally filled by the matter of the Moon ? 415
Did Pangea exist ? 414, 415
Why do both longest ridges emerge from the ocean near the North Pole ? 414, 402
1.1.3 Venus
Why does Venus not have ridges ? 410, 411
Why does Venus not have a magnetic field ? 409, 411
How can the atmosphere of Venus rotate so quickly ? 400, 391
Why is the velocity of the quick atmosphere zero on the surface ? 400
1.1.4 Mars
Why does Mars have no ridges ? 407-408
Why does Mars have the biggest volcanoes in the solar system ? 407
1.1.5 Jupiter and Saturn
Why do Jupiter and Saturn have strong magnetic fields ? 417
What can be the cause of the differential rotation of these Planets ? 385-386, 386, 394
Why is the differential rotation exactly perpendicular to the rotational axis ?
1.1.6 Comets
Why does the ion-tail point in antisolar direction ? 515-517, 519
Why does the "plasma-tail" not follow the solar, nonradial "frozen-in" field ? 452, 453
What is the origin of the ions of a comet ? 516, 515-519
Could a temperature of 4.6 MK of unknown origin cause the ions of Hyakutake ? 516, 517
Why did the small Tsuchiya Kiuchi emit X ray in 1990 as strong as Hyakutake in 1996 ? 515
How can the ion-tail consist of million km long filaments ? 519, 453, 515-519
Why are the filaments of the ion tail not unified or mixed by the solar wind ? 453, 519, 517
Why is the "antigravity" of the tail-ions 20 times stronger than the solar gravity ? 517
1.1.7 T-Tauri stars
What is the cause of the axial jets of the T-Tauri stars ? 644-646, 647
Why are the jets thin ? 78-80, 86, 368, 485, 644-646, 647,
Why does "neutral matter from the accretion disc" follow the axial magnetic field ? 664
Why do the jets have a circular cross-section ? 644-646, 647 (cf. "flat jet":339)
Why does the diameter of a jet slowly increase as it gets longer ? 644-647
Why are the material emissions not globular, similar to those of Eta Carinae 84, 644-647
Why are the jets aligned to the rotational axis ? 644-647
How can the star HH 34 eject only one jet since 200 years ? 644-646, 647
How can the star HH 34 eject a jet without an accretion disc ? 644-646, 647
Why are the knots in one jet not in the same distances from the star as those in the another jet ? 644
How can young stars constantly emit X ray 10 000 times above the solar level ? 646
1.2 Sun
1.2.1 The Sun as a process
Does any recent measurement show a stable Sun ? 96, 96-97
Is the solar rotation stable ? 60, 59-61, 132-142,
Is the solar diameter stable ? 62, 63, 149, 143-149
Is the solar irradiation stable ? 50, 349-352
Is the solar oscillation stable ? 152, 153
Did GALLEX exactly follow the decay of the radioactive As in 1997 ? 653
Is the solar neutrino flux stable ? 116-132, 53, 129, 141, 149, 653
Is the measured power of the solar core equal to the solar luminosity ? 116-132
Why are the solar non-magnetic parameters - e.g. the diameter - often shown
interpolated as curves ? 50, 53, 60, 62, 63, 96, 129, 141, 149, 152, 153, 653
Why do the curves of the non-magnetic parameters suggest a sunspot-periodicity ? 50, 53, 60,
Is any realized current-circuit of the "solar dynamo" known ? 285, 657
Is any estimation of the electric-current, -voltage, -power of the "solar dynamo" known ? 273
Does the poloid field - as "raw matter of the dynamo" - have a clear model ? 163
Is the differential rotation - as "drive of the dynamo" clear ? 417- 429
"How does the differential rotation react to the creation of the field ?" (Vial ) 289, 417 - 429,
"Where exactly is the " dynamo" situated ?" (Vial 1994) 21
How did the dynamo get started ? 284
Is the positive feedback of the solar dynamo clear ? 287
Did SOHO find the "solar dynamo" or any of the "deep flux tubes" ? 313
How can the "dynamo" "produce" big sunspots and also 150 km thin flux tubes ? 377
How can the "dynamo" produce 1 million km thick flux tubes ? 550 - 551
How can the "dynamo" produce and store many thick flux tubes ? 550 - 551
How can the "dynamo" produce 20 thick and radial flux tubes simultaneously ? 550-551
Which "dynamo" produces the flux tubes of the comets ? 453
Which "dynamo" produces the flux tubes of Abell 30 ? 269
Which "dynamo" produces the flux tubes of supernova-remnants ? 662
Which "dynamo" produces the gigatesla field of the neutron stars ? 679
Which "dynamo" produces the long and thin magnetic field of the radiogalaxies ? 667, 669
Which "dynamo" produces the filaments of the superclusters ? 641
1.2.2 Solar wind
What releases the solar wind ? 9-14, 20, 21,
Gravity ? Nuclear forces ? Magnetic force ? 436-438, 437,
Magnetics, perhaps via MHD-waves ? 444 - 446,
Why did SOHO not find the source of the MHD-waves ? 445
Can the coronal heat be the source of the solar wind ? 19-23, 98, 438-443, 440
Is the solar wind neutral, positive or negative ? 19-23, 68-72, 71, 446-463
Why is the solar wind invisible in all wavelengths ? 524
Why are coronal holes "holes" ? 463
Why does the solar wind have a velocity of about 750 km/s ? 464
Why do the coronal holes mostly appear near the poles ? 465
Why does the wind seem to have a temperature over 1 MK ? 466
Why does SOHO show oxygen ions of 100 MK in the solar wind ? 467-469
Where is the "coronium light" in the aurora ? 469
Why is the solar wind not 40 MK hot ? 469
Why are the polar streamers thinner outwards ? 470-472, 470
Why do the polar streamers strongly diverge ? 472-473, 474
Why did Ulysses find ions in the wind in a 5 minute-rhythm ? 473
Why does the Sun have helmet streamers in sunspot-minimums ? 473-477, 474, 477
How can the helmet-streamers be asymmetrical to the solar equator ? 477, 478
How can helmet streamers exist in close vicinity to each other ? 479
Why are polar streamers thin but helmet streamers thick ? 479
Why is the coronal hole black in X ray but bright in 1083.0 nm ? 80, 15, 480
Why are coronal holes black but the corona bright in X ray ? 31
Why are all coronal holes equally black in X ray ? 15, 80, 92,188, 190, 297, 501, 504, 480
Does the solar wind have a "supersonic" speed ? 484
Did Ulysses detect the solar explosions ? 485
Why is the solar wind not braked by the gravity and by its expansion ? 488, 495
How can the solar wind "blast" within seconds ? 491
What is the cause of the slow and fast the winds ? 492, 495
Why does the "polar wind" have a high velocity ? 494, 495, 496
Why was the solar wind constantly very slow at Jupiter ? 497, 495, 498
Did Ulysses observe the Jovian electron torus ? 498,499, 500
Did Ulysses observe a CME ? 499, 500
Why did the solar wind "flow" faster and faster in 1993 ? 504, 502-506, 506
Why does the wind-curve show the solar rotation distinctly ? 504, 507, 507-508
Why was the wind slow (350km/s) in the ecliptics in 1995 ? 499, 501, 504 508-510
Why did Ulysses find quick reversals of the solar poloid field ? 510-512
Why does the "magnetic field frozen-in in the wind" alternate ? 513, 514, 512
Why do the coronal holes have a unipolar magnetic field ? 518
Why did two large coronal holes appear in 1974 ? 493, 507, 522, 523, 520-524
How can coronal holes rotate rigidly ? 522, 523, 521-524
Why does the aurora not appear in sunspot-minimum ? 524
Why do the aurora simultaneously appear on both poles of planets ? 24
Why are only few positive ions in the coronal holes ? 18
Why is the flux of the cosmic rays higher in sunspot-minimum ? 93, 95, 19,
1.3 Mathematics
Several of such questions are answered in only 1-2 pages in their related chapters:
| solar and planetar poloid fields | flux tubes |
| corona | sunspots |
| flares | flare stars |
| radiogalaxies | gamma ray bursts |
| supernovae | solar loops |
| cosmology |
Some last questions at the chapter Mathematics dealing with the birth, life and death of neutron stars are given here:
How can free protons cover the neutron body during the implosion ? 678
Why can a positive neutron star not produce more than about 30 gigatesla ? 678 - 680
How can a neutron star have the probably highest voltage of the Universe of +1025 V ? 685
Why do the youngest neutron stars have the highest voltage and highest magnetic field ? 689
How does a neutron star produce the particles of the cosmic rays ? 685 - 686
How does a neutron star accelerate the particles of the cosmic rays ? 685 - 686
Why can a shock front not accelerate the cosmic rays to almost light velocity ? 688
Why can enclosed protons produce magnetic and rotational changes breaking out ? 687 - 688
How can a neutron star release all functions of a soft gamma repeater ? 689
2.0 Why is the flux of cosmic rays higher in sunspot-minimum?
Forbush discovered, 5 decades ago, that the flux of cosmic rays is anticorrelated to the solar activity. It is almost proportional to the sum of the areas of the coronal holes (2.02).
The particles of cosmic rays are atom-nuclei with almost light velocity. They are atoms without electrons: e.g. C VII, O IX, but surprisingly, the cosmic rays contain much less than 90% protons and only about 1% alpha-particles and 1% electrons (CA 1994 p. 322). In chapter M, the electric origin of the cosmic rays at the neutron star is described. This model explains these strange abundances and almost pure (>99%) positive charge.
In sunspot-minimum, the solar surface is made strongly negative by the thermoelement-electrons, because, few positive ions appear in X ray bright points and in other coronal fields. (These ions neutralize a huge amount of the free thermoelement-electrons in sunspot-maximum.) In minimum, the mostly negative solar surface attracts the positive particles of the cosmic rays, electrically, even those from long distances, from light-weeks away. Also those positive particles which would have bypassed a neutral Sun, hit the negative Sun. The cosmic ray flux will be high (2.02) on the Sun and naturally also on the Earth. In the Maunder Minimum, the cosmic ray flux was maximum in the last two millenia (4.59-4.60), shown by 14C in tree rings (5.03).
The explanation with "a magnetic dispersion" of the perfectly dispersed cosmic rays will be refuted later (2.03-2.04).
3.0 What releases the stellar wind?
The thermoelement-electrons continually arrive at the solar surface due to the continual existence of the solar temperature difference between the solar core and surface and due to the almost infinite number of 0.6 x 1060 electrons in the core. All other solar particles with mass (e.g. protons) are at least 1836 heavier than the electrons. Iron ions are more than 100 000 times heavier than the electrons. The more than 316 times slower iron ions (316² = 100 000) remain in the depth, the electrons come out (see equation 1).According to my new thermoelement-law i.e. to the electric astronomy, the thermoelement-electrons surface continually. These more and more thermoelement-electrons cannot be stored on the solar surface. They release a continual electrostatic explosion on the solar surface due to the very strong electric repulsion among these free thermoelement-electrons. Every new surfaced electron repulses all already surfaced electrons upwards. Also the already upwards flying electrons in the free space are repulsed with the electric force which is much stronger than their gravity (table 2.2). This process is similar to the continually injected kerosine in a jet-motor. A continual explosion is the result (1.04). These electrons in charge overbalance drag along light matter from the surface with a high velocity of 750 km/s. electric force which is much stronger than their gravity (table 2.2). This process is similar to the continually injected kerosine in a jet-motor. A continual explosion is the result (1.04).
These electrons in charge overbalance drag along light matter from the surface with a high velocity of 750 km/s.
Vice versa: no other force could accelerate this flow of about 1 million ton matter/second to the velocity of 750 km/s.
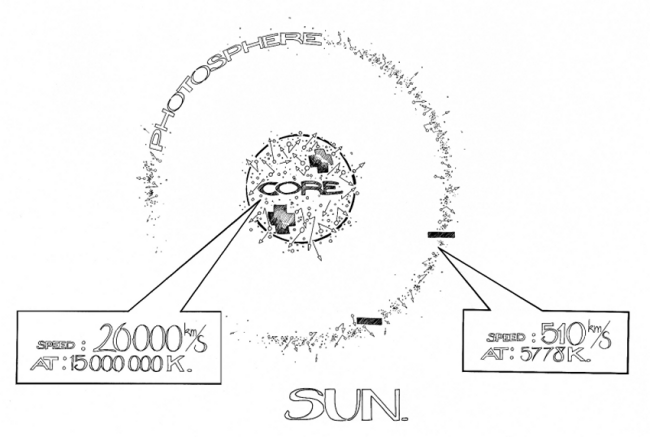
3.1 The Sun as a thermoelement In the solar core of about 15 MK, the electrons (small spheres with zig-zag velocity arrows) have an average thermal velocity of 26 000 km/s (equation 1). The protons (points) are much slower. The thermal electron-velocity is only 510 km/s on the surface according to the Boltzmann-law. The result is that the hot particles and the strong photons continually push out the electrons from the core. The surfaced electrons hardly find a way back. The HRD-stars are similar to an atom: their small but heavy core is made positive (++) by the lost electrons and the big body is made negative by the electrons which wander to the surface, see big "minus" signs. (Particles are not shown between core and surface.)
The difference between the masses of electron and proton causes automatically the the solar wind ! Its measured velocity of 750 km/s can be calculated for the very first time !
This very quick solar wind cannot be understood without the new thermoelement-law. Astronomy Prof. K.R. Lang (1995) "We do not understand the basic driving mechanism of the solar wind." (p. 123.)
I hope that my readers are happy. My new thermoelement-law simply and automatically explains "the basic driving mechanism of the solar wind". It explains also all wind-measurements of Skylab, IMP-8, Ulysses in all details. It is evolved in the chapter on the wind.
The electric circuit of this solar thermoelement is very simple:
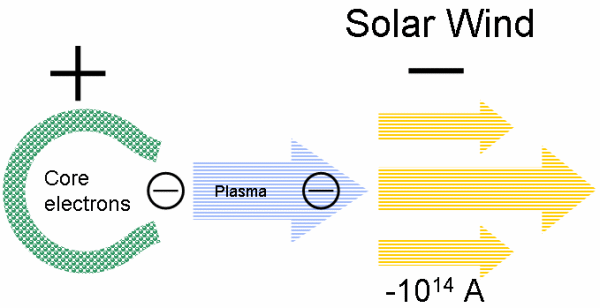
3.2 The electric circuit of the stellar thermoelement A very small amount from the 0.6 x 1060 core-electrons are pumped by the temperature difference from the core (left) through the plasma (line) into the infinite space as stellar wind (right). This solar thermoelement delivers a negative direct current of -1014 A into space from its negative pole (on the right) since gigayears. This electric wind drags-along light matter (hydrogen, 4% helium, protons, alpha particles but no magnesium (see Ulysses) and no heavy elements. This is the negatively charged solar wind (see chapter 4.5).
The thermoelement electrons come out from the Sun not due to the 2 000 V thermovoltage, but the thermovoltage is the result of the pushed electrons in the Sun. The same is valid in all other terrestrial or celestial thermoelements.
Not a section of the Sun is a dynamo (which has no circuit !) but the whole Sun is a simple thermoelement-generator (with a simple circuit). The temperature difference is directly converted to electric energy as in the Pu-batteries of the spacecrafts. No mechanic drive as in the alleged solar dynamo is necessary.
In this new and electric astronomy, the inexplicable dynamo is totally substituted with the simple thermoelement.
It is not anymore necessary to look for the dynamo´s position in the Sun. Where is the dynamo ? Is it:
- just below the surface (Babcock, Parker, Leighton 1950-1960),
- deep in the convection zone (Kusserow, Denzer 1980-1990)
- just below the convection zone in the rigid body, in the depth of 220 000 km (Scherrer 1997)
- in the core (Lang 1995, Grandpierre 1996)
The "solar dynamo" is nowhere in the Sun.
The whole Sun is a thermoelement-generator.
All thermoelement-parameters are measurable. The current of this thermoelement is transported by the solar wind.
The solar thermoelement does not produce inductive current. It needs only temperature difference, not rotation. This generator is absolutely not braked by the induction according to the Lenz-law.
The wind moves antigravitationally. An electrically neutral explanation has only the heat-motion which can move upwards. Particles should push particles in all directions, also upwards. This electrically neutral wind would be a neutral thermal evaporation of the hot solar surface.
But the thermal cause of the fast solar wind should have a temperature of 24 MK according to the Boltzmann-equation0.5 mv² = 1.5 kT (1)(M. 01). However, this very high temperature is nowhere to be found on the surface (nor in the whole Sun).
Parker supposed only 2 MK. But this is also non-existent on the surface and not detectable as emitted mass in the heliosphere. The corona, as a wind-source, is impossible due to the fact that the solar wind exists (it is even strongest, then) when no corona is present (4.67).
Yohkoh´s and SOHO´s sharp pictures do not show a trace of an evaporating process of the coronal loops. These beautiful pictures were not available in Parker´s time. According to the electric model, the corona is not hot but positive (see below). Naturally, a positive corona cannot emit a negative wind.Instead of the heat, the wind-particles are simply emitted and accelerated electrically in a cold way. Their direction in this model is automatically correct: only upwards (4.47) and not in all directions as in the case of an evaporation ! These particles do not collide, they fly on parallel orbits, along the electric field. This is why they do no emit electromagnetic waves while flying along their almost straight orbits. The Sun is similar to an electrostatic paint-jet, not to a torch paint-jet.
The stellar wind is negatively charged, therefore, it has no recombination light: it repulses electrons. During 9 eclipses of the Maunder Minimum the solar wind was invisible for unaided eyes. But it would be also undetectable in X-ray.
However in the present time, the wind drags along positive ions from X ray bright points which appear always separated on the poles (4.56, 4.68). This electrostatically attracted positive matter has also no collisions, but it has recombination light, and therefore, it is visible as "polar filaments" during the eclipse (4.56) or in EUV (1.10, 4.10). These filaments makes the wind and the electric field indirectly visible similar to aluminium slices fluids or air (4.30). These positive filaments are no components of the negative wind. Their "temperature" of 1.5 MK (table 4.8) is not the "temperature" of the wind. They are also no "somehow transformed" magnetic force-lines. The "polar magnetic force-lines" were not found by Ulysses.
Here again, the energy of the windprotons (M) corresponds to 24 MK and not 1.5 MK or 2 MK (M.01). But, the stellar wind is no moving gas and its motion energy is not transformed to heat.